Abstract: 本章介绍线性代数的核心内容,关于Vectors Space和subspace的一些观点,本文作为第一篇,主要说明基础知识
Keywords: 向量空间,子空间,列空间,张成
开篇废话
好几天没有更新博客了,前天本来想写,发现环境出现点问题,因为我本身对网站知识并不是很了解,hexo g的时候有个warning,我就开始修,结果很简单,直接修的全是error,好在都有备份,昨天就重新搞了一下,总体来说hexo对于使用来说还是比较简单的,所以一上午也就差不多搞定了,今天开始写线性代数最重要的一部分,也有点困难,所以我决定写的慢一点,啰嗦一点,必要的时候把前面的东西重新拿过来,数学很难,如果之前的知识掌握不住,后面的基本就是云里雾里,但是哪个学科不是这样呢?所以,融会贯通,回头来看,就会豁然开朗了
向量空间(Spaces of Vectors)
向量空间,我刚又看了一下Pro. Strang老爷子的书,很遗憾,没找到定义,可能是受封建教育搞得不来个黑体字定义,就不知道啥是啥了,通俗的解释下吧。
我们都认识向量
$$
v=\begin{bmatrix}1\\2\end{bmatrix}
$$
他的一般形式呢,就是一个向量含有两个实数元素,这里写的1和2也可是250和520,只要是实数,这个向量都是在一个圈子里,这个圈子呢就是我们的小标题,向量空间,一个向量空间包含无数组向量,但是这些向量必须满足一定的规则,并且向量空间作为一个类,有自己的固有属性,我假定你对面向对象的编程有些了解,所以说出了类和对象之类的名词,不专业,但是能形象一点,方便大家理解。
$$
v=\begin{bmatrix}x_1\\x_2\end{bmatrix}\\
x_1,x_2 \in \Re
$$
可以看出,这个向量是个二维的向量,那么我们把这个向量空间写成:
$$
\Re^2
$$
怎么样,眼熟么?惊喜不惊喜,意外不意外?
我刚才说了,这是个特殊的例子,但是也说明了一定的规则,首先元素要满足一定范围,可以是实数,可以是复数,也可以不是数字,比如可以是函数,或者其他任何东西。
脑洞时间:那么我有一个问题,如果每个元素都是不一样的东西,这个能算向量空间么?比如
$$
u=v=\begin{bmatrix}book\\food\\number\end{bmatrix}\\
$$
在python里这些可以组成list,我们慢慢看看,这个”向量空间””是否满足所有条件!
$R^n$
$$
v=\begin{bmatrix}x_1\\x_2\ \vdots\\x_n\end{bmatrix}\\
x_1,x_2, \dots ,x_n \in \Re
$$
所有元素属于实数,并且有n个元素,那么我们可以得到我们的向量空间
$$
\Re^n
$$
这个可以根据上一节的结论进行推演,把2换成了n,其中n是确定的常数
$C^n$
$$
v=\begin{bmatrix}c_1\\c_2\ \vdots\\c_n\end{bmatrix}\\
c_1,c_2, \dots ,c_n \in C
$$
所有元素属于复数,并且有n个元素,那么我们可以得到我们的向量空间
$$
C^n
$$
这个可以根据上一节的结论进行推演,把实数换成了复数,其中n是确定的常数
M,F and Z
同理,元素可以属于任何其他域,比如可以使矩阵,函数,或者是0
M:The vector space of all real 2x2 matrices
F:The vector spcae of all real functions f(x)
Z:The vector space that consists only of a zero vector
这里面有个比较特殊的是F好吧,我承认都挺特殊,但是F是个无限维函数空间,
一个与F类似,但是维度有限的例子是多项式空间$P$或者$P_n$
$$
a_0+a_1x+a_2x^2+\dots+a_nx^n
$$
Z向量空间值得说一下,我们平时可以把它写成
$$
\Re^0
$$
他的维度是0,维度说了半天发现好像前面没说过什么是维度,那后面补上。Z是最小的向量空间,所有空间必须包含0向量,但是每个空间的零向量都不相同,根据自己的特点来产生0向量的形状。
8 Conditions(八项基本原则)
来来来,现在该说正事了,刚才举了几个例子,都是从书上抄的,那么到底什么样的空间才能是空间呢?或者说我们脑洞问题怎么才能解答?首先向量空间可以不是数字组合出来,但是必须遵守八项基本原则(8 conditions)
八项要求:
1、要同党中央保持高度一致,不阳奉阴违、自行其是;
2、要遵守民主集中制,不独断专行、软弱放任;
3、要依法行使权力,不滥用职权、玩忽职守;
4、要廉洁奉公,不接受任何影响公正执行公务的利益;
5、要管好配偶、子女和身边工作人员,不允许他们利用本人的影响谋取私利;
6、要公道正派用人,不任人唯亲、营私舞弊;
7、要艰苦奋斗,不奢侈浪费、贪图享受;
8、要务实为民,不弄虚作假、与民争利。
这个是他们主流的八项原则,我们的是非主流的,哈哈
1: $x+y=y+x$
加法交换律
2: $x+(y+z)=(x+y)+z$
加法结合律
3: 存在一个0向量满足:$x+0=x$
加法0向量,加上任何向量都等于这个向量本身
4: 对于所有x存在$-x$满足$x+(-x)=0$
加法反向量(这个名字是我想的),就是能够找到一个向量,使得其与原始向量相加为0
5: 1乘以$x$要等于$x$
乘法1向量,乘以谁就得谁
6:$(c_1c_2)x=c_1(c_2x)$
乘法结合律
7:$c(x+y)=cx+cy$
乘法分配率,注意这个c是数,不是向量
8:$ (c_1+c_2)x=c_1x+c_2x$
乘法分配率,上面的分配的是scalar,这个分配的是向量,$c_1,c_2$是数字
那么判断是不是向量空间的任务就变的有依据了,我的脑洞显然不是,比如book里面就没有anti-book可以把书变没。
FMZP这几个家伙就都满足,不信你就自己试试,我试过,没问题!
Subspace(子空间)
子空间肯定对应有父空间什么的,实际上没有,因为sub前缀根本就没有继承的意思,而是说是个小一些的,包含少一些的,所以子空间对应于他的上一级空间,少了一些东西,准确的说是少了很多东西,这些东西就是向量,比如一个平面,那么平面上的一条线,他是平面的一部分,但是只是一小部分,就是这种关系,书上的描述是a vector space inside $\Re^n$ ,those are Subspace of $\Re^n$。
A subspace of a vector space is a set of vectors (include 0) that satisfies two requirement: if v and w are vectors in the subspace and c is any scalar ,then
(i) $v+w$is in the subspace
(ii) $ cv$is in the subspace
以上(i)(ii)是判断子空间的重要标准,这个也是我们之前提到的,线性代数最最最最最基础的最关键的两种计算。
Linear combination中详细的描述了这两种计算。子空间主要强调closed,在加法和乘法上封闭,你不能两个空间内的向量,加乘出了空间,飞翔到外太空,这样就不能称为子空间了,概括一下子空间就是包含在某个空间内,自身对于加法和scalar封闭的这么一个空间。
Some Facts:
1:当(ii)中c为0的时候0向量在空间内,也就是说子空间必须包括0向量
2:如果向量v,w在子空间内,那么其线性组合$cv+dw$一定也在子空间内
3:一个三维空间,过原点的直线是子空间
4:0向量是一个空间的子空间
子空间是个相当有用知识,在《线性代数应该这样学》中就是从空间这个切入点来建立整个线性代数体系的。书上主要通过二维和三维的例子来介绍子空间的,比较容易理解。
Column space of A(矩阵A的列空间)
A是个矩阵,有m行,n列,每行有n个元素,每列有m个元素,刚开始学数字图像处理的时候,总是分不清行和列,高和宽是啥。哈哈哈,还记得我们的矩阵乘法么?我们首先研究的是$Ax=b$里面的”Column Picture”就是列空间的一种体现,也就是把A中的每一列当做空间内的一个向量,通过(ii)的方式组合出的新向量 $\textbf{b}$一定也是在A的所有列所在的空间内,这就是列空间。
The column space consists of all linear combinations of the columns.The combination are all possible vectors $Ax$.They fill the column space C(A)
所以Ax=b如果关注x就是解方程组,如果关注b就是列向量空间,当然,这两个的主要决定因素还是A,如果b在A的列向量空间内,也就是某个$x_1$线性组合A的列,得到$b_1$,那么这个$Ax=b_1$的解存在(唯一不唯一不一定),而且$x_1$是一个解;这又引出了另一个大课题,$Ax=b$到底特么的有多少个解?!
the system $Ax=b$ is solvable if and only if b is in the column space of A
举一个🌰::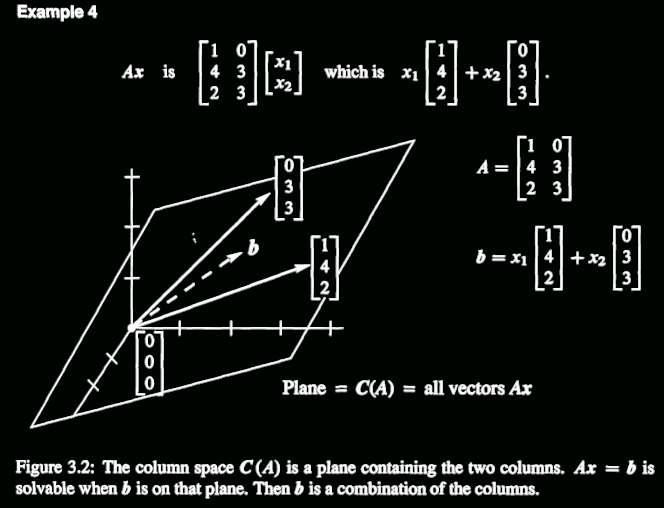
例子就是上面那段话的正规描述。
Span(张成)
张成,tensor翻译成”张弛”,搞得数学名词都姓张,但是张成这个词还是比较形象的,想象一把伞,散的骨架有很多细的支撑骨架,一打开,张成一把伞,其实这个很形象;如果你有棍子和布,如果有一根棍子,你只能撑出一个直线(晾床单模型),如果两个棍子不摆在一条直线,你可以撑起一个面,如果你有三根棍子(两两不在一条直线),就可以撑出一个四面体,一个三维图形,棍子就张成了对应的空间。这个有点牵强附会,但是可以简单的类比一下,向量也是,两个不在同一条直线上的向量,就能通过线性组合,组合出他们张成平面上的所有向量,对于更高维同理。对于矩阵A的n列,他们可以张成n维空间,或者小于n维的空间,当m(行数)>n(列数)那么就是 $\Re^m$的n维(或者小于n维)子空间。
描述的有点啰嗦,如果能听懂最好,听不懂就可以去看看书了。
S = Set of vectors in V($v_1,v_2,v_3,\dots$,v_n)
$$
SS=c_1v_1+c_2v_2+\dots+c_nv_n
$$
其中 $\textbf{c}$ 可以使任何实数,我们就说SS是S张成的,并且SS是S所在空间的一个子空间。
张成对应基的概念在下一课。
Definition: A set of vectors spans a space if their linear combinations fill the Space
Conclusion
这篇有点长啊,写了三天,当然是断断续续的,如果阅读不连贯也是正常的,这个是线性代数的核心内容,希望对大家有帮助。
