Abstract: 本文是关于Bayes’ Theorem 的介绍性知识
Keywords: Bayes’ Theorem，Law of total Probability

贝叶斯定理

今天的废话可能有点正经，就是关于Bayes’ Theorem的相关往事，做人脸识别的都会知道一个叫做联合Bayes的分类器，没错，我们当时做的时候也是第一个做了这个算法，当然，我没有自己去研究实践，最后结果不太理想，当然我不是说我去做结果就能好多少，其实投资也好做项目也好，失败向来不可怕，各种各样的死法在开始之前都有些预期，但是我们有一个期待，就是自己有个主观概率觉得我有90%可能会成功，前提是xx个项目能够顺利如期成功，但是当xx项目进展严重受阻，你就会重新评估成功概率，这个过程就可以用Bayes定理去建模；这个过程其实不可怕，最可怕的是你不知道你现在遇到了什么问题，你的小伙伴告诉你成功了，但其实根本没成功，有时候告诉你没成功，但是其实已经成功了，当一些事件结果变得不可信，那么你的评估将会变得毫无意义。
失败不可怕，可怕的是你不可控，说赚了三块钱，结果赔了五块，说赔了五块，结果赔了八块。

贝叶斯定理 Bayes’ Theorem

上面一个经典案例中包含了两个Bayes相关的经验，首先是一个具体的算法，用于分类，另一个是实现这个算法的过程产生的故事，也可以用贝叶斯公式来建模。
贝叶斯公式在概率论和统计中处于非常核心的部分，所以才有贝叶斯学派这种派系（不知道在我们社会主义伟大祖国，搞个这种学派是不是违法的）对立学派是频率派，这两派具体怎么样我们先不去深入区分，因为我们目前研究的境界还不需要站队，而就算有一天你需要站队了，这种站队可能出于利益和权利的考虑也要少很多，而是更多的源自自己觉得哪一派更接近真理。

频率学派的观点主要是认为所有事件的概率都不确定，但是可以用频率来近似得到。
贝叶斯派则认为所有事件的概率都是确定的，只是你的先验知识不足，所以算不出来而已。

大概可以这么理解，我们不再纠结上面这个关于上帝存不存在的问题，回到数学本身。

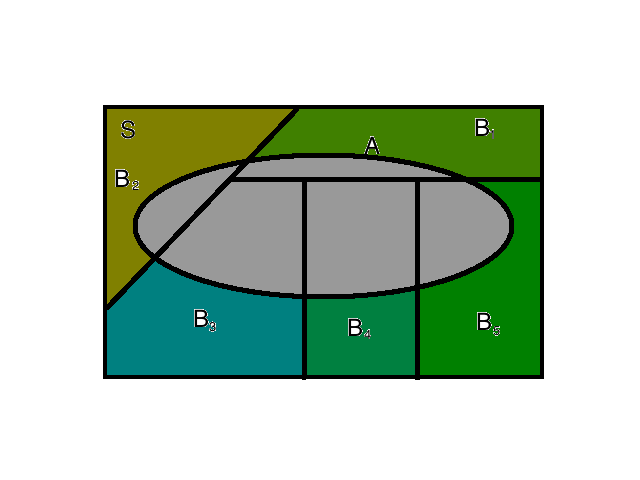
例如上图，来自全概率公式那一篇：当我们面对一个试验，在所有的partition中（ $B_1\dots B_n$ ）必然有一个将要发生，但不确定发生哪一个，我们可以观察到另一个事件A，如果已知$Pr(A|B_i)$ ，那么当我们确定A事件的发生概率的时候，就可以翻过来推到每个partition发生的概率有多大$Pr(B_i|A)$
上面这个是简单的逻辑分析，可以大概知道我们为啥要Bayes公式。

从分析上通过前面的条件概率公式可以非常轻松的得到贝叶斯公式：
$$
Pr(A\cap B)=Pr(A|B)Pr(B)=Pr(B|A)Pr(A)\\
Pr(A|B)=\frac{Pr(B|A)Pr(A)}{Pr(B)} \quad where \quad Pr(B)\neq 0\\
or\\
Pr(B|A)=\frac{Pr(A|B)Pr(B)}{Pr(A)} \quad where \quad Pr(A)\neq 0
$$

这个就是最简单的贝叶斯公式推到，同时可以用全概率公式进行代换，就能得到更专业的贝叶斯公式。
举个例子🌰 ：

还是前面的随机拿螺丝，两个箱子A和B，我们随机选取一个箱子从里面拿螺丝(箱子有相等的概率被选中，所以 $Pr(A)=\frac{1}{2}$ )，已知A中有长螺丝6个短螺丝4个，B箱子有长螺丝3个短螺丝7个，设长螺丝为事件L短螺丝为事件S，那么可以有
$$
Pr(L|A)=\frac{6}{10}\\
Pr(S|A)=\frac{4}{10}\\
Pr(L|B)=\frac{3}{10}\\
Pr(S|B)=\frac{7}{10}\\
Pr(L)=Pr(L|A)Pr(A)+Pr(L|B)Pr(B)=\frac{6}{10}\times \frac{1}{2}+\frac{3}{10}\times \frac{1}{2}=0.45\\
Pr(S)=Pr(S|A)Pr(A)+Pr(S|B)Pr(B)=\frac{4}{10}\times \frac{1}{2}+\frac{7}{10}\times \frac{1}{2}=0.55
$$
现在我们已知拿出了一个长的螺丝，那么问从A箱子拿出来的概率是多少，从B箱子拿出来的概率是多少。
$$
Pr(A|L)=\frac{Pr(L|A)Pr(A)}{Pr(L)}=0.3/0.45=0.667\\
Pr(B|L)=\frac{Pr(L|B)Pr(B)}{Pr(L)}=0.15/0.45=0.333
$$

得出结论是A的可能性更高，因为A中长螺丝更多，这与我们的感觉上是一致的。

Theorem Bayes’ Theorem: Let the events $B_1\dots B_k$ from a partition of the space S such that $Pr(B_j)>0$ for $j=1,\dots ,k$ and let A be an event such that $Pr(A)>0$ , Then for $i=1,\dots,k$ :

$$
Pr(B_i|A)=\frac{Pr(B_i)Pr(A|B_i)}{Pr(A)}=\frac{Pr(B_i)Pr(A|B_i)}{\sum_{j=1}^{k}Pr(B_j)Pr(A|B_j)}
$$

这个就是普通的Bayes公式结合上全概率公式得出的一个比较实用的版本，证明这里就不详细写出来了，因为通过条件概率和全概率公式就能得出上面的结论，那么如此简单的一个公式为什么如此核心呢？
我们从哲理中分析一下，首先我们看 $Pr(B_i)$ 从本文第一张图片上可以看出来，这个划分从客观上说是是对完整样本空间的一个分别估计，这个过程与A是否发生无关，但当试验被观察到事件A发生了，我们的样本空间实际上发生了改变，不在是完整的S，因为$A^c$ 不可能发生了，这种情况下，我们将这个分割重新计算：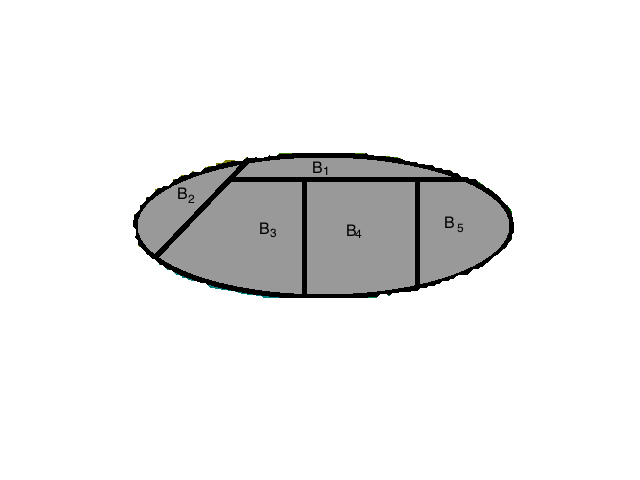

这个图是从上面的那幅图啃出来的，所以有点不整齐，这个整个过程就是贝叶斯要刻画的，样本空间的改变导致了整个划分的概率发生了不确定的变化，以前大的可能现在变得小到没有，现在大的可能之前非常小。

一般情况下，我们在实验开始之前已经知道了样本空间，以及它的“划分”，如果观察到某个划分发生了，我们可以相应的变更我们所关注的事件A，这是一般上的从原因推出结果，典型的概率论过程，已知原理推结果。

实际上我们不可能，也没能力知道这个划分，但是结果我们只要观察可能定能看到，于是我们通过结果A来反过来推这个划分是什么样子的，那么这个过程是个典型的数理统计过程，已知结果推原理，也叫贝叶斯统计。

条件贝叶斯定理 Conditional Version of Bayes’s Theorem

所有概率公式定理都可以改装成条件版本，Bayes’s Theorem也不例外，当然和原始公式基本一致：

$$
Pr(B_i|A\cap C)=\frac{Pr(B_i|C)Pr(A|B_i\cap C)}{\sum^k_{j=1}Pr(B_j|C)Pr(A|B_j\cap C)}
$$

对于扩展到条件概率，我们一般的做法就是给所有项的条件上都并上一个附加的事件。

先验概率，后验概率 Prior and Posterior Probabilities

我记得大学的时候学概率论的时候，第一次学贝叶斯公式，那时候老师跟我们说贝叶斯的每一项都有一个名字，先验，后验，似然值什么的，那时候没心思学习数学理论，考试的时候只能去背一下，结果一直也不知道啥意思，后来干活的时候，也遇到过Prior filter 和posterior filter，当时只知道一个前置滤波器，一个是后置滤波器，当看DeGroot的书的时候，看到Prior Probability和Posterior Probability才知道原来这个先验概率和后验概率是先于试验和后于试验的意思，很明显，等号前面的那个是要求的，肯定是试验后要计算的，肯定是后验概率，分母上的$Pr(B_i)$ 这个划分明显是试验之前知道的，故而叫做先验概率。

多步后验概率计算 Computation of Posterior Probabilities in More Than One Stage

这部分可以看做是个应用但是很有实际意义：
两个硬币，一个是正常的,A,两面不同 ${H,T}$ ，另一个是特制的B，两面相同都是 ${H}$ ，在我们不知道拿出了哪个硬币的前提下，丢硬币，第一次出现了$H_1$ 是个H，下标表示试验步数，那么我们可以使用贝叶斯计算：

$$
Pr(A|H_1)=\frac{Pr(H_1|A)Pr(A)}{Pr(H_1|A)Pr(A)+Pr(H_1|B)Pr(B)}=\frac{\frac{1}{2}\times \frac{1}{2}}{\frac{3}{4}}=\frac{1}{3}\\
Pr(B|H_1)=\frac{Pr(H_1|B)Pr(B)}{Pr(H_1|A)Pr(A)+Pr(H_1|B)Pr(B)}=\frac{1\times \frac{1}{2}}{\frac{3}{4}}=\frac{2}{3}
$$

这是第一步的结果，那么如果我们继续丢同一个硬币，观察结果，我们得到了$H_2$ 还是一个H，那么我们将得到条件版本的贝叶斯用法：
$$
Pr(A|H_1\cap H_2)\\
=\frac{Pr(H_2|A\cap H_1)Pr(A\cap H_1)}{Pr(H_2|A\cap H_1)Pr(A\cap H_1)+Pr(H_1|B\cap H_1)Pr(B\cap H_1)}\\
=\frac{Pr(H_2|A\cap H_1)Pr(A|H_1)Pr(H_1)}{Pr(H_2|A\cap H_1)Pr(A|H_1)Pr(H_1)+Pr(H_1|B\cap H_1)Pr(B| H_1)Pr(H_1)}\\
=\frac{Pr(H_2|A\cap H_1)Pr(A|H_1)}{Pr(H_2|A\cap H_1)Pr(A|H_1)+Pr(H_1|B\cap H_1)Pr(B| H_1)}
$$
上述过程对于B是一样的，通过条件概率的公式，可以化简得到上述公式，通过对比，我们发现两步的差别就是第二步的Prior 是第一步的posterior，如果是多步的试验，可以完全满足这个规律上一步的posterior用作下一步的prior
这种和我们现实中的各种推理完全符合，我们通过推理分析，修改了我们最初的估计，并实现在估计更接近事实，这就是个进化过程。
计算得出我们第二步的结果：
$$
Pr(A|H_1\cap H_2)=\frac{1}{5}\\
Pr(B|H_1\cap H_2)=\frac{4}{5}
$$
这是符合我们的感觉的，出现H越多，A的可能性就越低。

条件独立事件 Conditionally Independent Events

概要观察上面这个丢硬币的例子，$H_2$ 的出现和 $H_1$ 的出现应该是相互独立的，但是结合上面的计算我们发现当$H_1$ 发生的时候，$H_2$的不确定性被影响了，所以在A和B不确定时，并不独立，但是当我们确定是一个正常的硬币，也就是A确定发生的时候，$H_1$ 和 $H_2$ 独立。
而且我们观察上面的计算过程，如果我们继续算下去，当前步骤的先验概率（上一步中的后验概率）会逐渐收敛，而不论初始值是什么:

N = 10

P_a_=0.5
P_b_=0.5

for i in range(N):
    P_a_hi_=(P_a_*0.5)/(P_a_*0.5+P_b_*1.0)
    P_b_hi_=(P_b_*1)/(P_a_*0.5+P_b_*1.0)
    P_a_=P_a_hi_
    P_b_=P_b_hi_
    print "$Pr(A|\\bigcap^"+ `i` + " H_i" + ")=" + "%0.6f" %P_a_ + \
          ";Pr(B|\\bigcap^"+ `i` + " H_i" + ")=" + "%0.6f" %P_b_ +"$"

跑了下结果：

当$Pr(A)=0.5$ 和 $Pr(B)=0.5$ 时：

当次数足够多的时候，会收敛到一个常数值，为什么呢？我们可以去研究一下他的递推公式
$$
x_i=\frac{ax_{i-1}}{ax_{i-1}+b(1-x_{i-1})}
$$
没算出来具体怎么收敛，数分还没学好，如果后面会了回来算一下。

补充个例子：

某种病毒在人口中的携带率是$Pr(pv)=0.03$ (pv,nv分别代表携带病毒和不携带病毒)检测的时候中会出现一下情况（有机器学习经验同学会对这个非常熟悉，包括True Positive (TP)，False Positive (FP)，False Negtive (FN），True Negtive (TP)）：
$$
Pr(P|pv)=0.99\\
Pr(P|nv)=0.05\\
Pr(N|pv)=0.01\\
Pr(N|nv)=0.95\\
$$
当假定某人被检测其携带病毒，那么此人携带病毒的概率是多大？

我们没文化，根据实验说明，我们有99% 的概率携带病毒，如果病毒致死律很高，这个概率足以让你准备后事。
如果我们有文化，考虑下先验知识，病毒本身携带率那么低，当我们被检出携带病毒，那么我们结合携带率和实验准确度，可以得出：$Pr(pv|P)=\frac{Pr(P|pv)Pr(pv)}{Pr(P|pv)Pr(pv)+Pr(P|nv)Pr(nv)}=\frac{0.03\times 0.99}{0.03\times 0.99+0.97\times 0.05}=0.380$ ,这个看起来还可以抢救一下

这种实验的关键是提高准确率也就是0.99需要更高比如0.9999999，这是后检测结果更接近真实结果，0.99会产生大量虚报，这个在机器学习上非常有用！

人工智能基础

【概率论】2-3:贝叶斯定理(Bayes' Theorem)