Abstract: 本文介绍期望的条件版本,也就是条件期望
Keywords: Expectation,Prediction,Law of Total Probability
条件期望
说到条件,我们前面反复说,所有概率都是条件的,随机变量也是,那么这几天我们学到的各种数字特征就应该也有条件版本,而我们学的这几个数组特征都是建立在期望的基础上,所以我们只要研究了条件期望,其他各特征的条件版本就是在此基础上的函数版本。
本文还有一个重要的部分就是prediction——预测,机器学习的除了发现事物本身内在的原理,另一个目的就是预测,而我们要预测的这个变量可能我们并不知其分布性质,而是知道另一个跟他有关系的随机变量的分布,那么我们就要用到全概率法则的条件版本了,具体我们来详细说清楚
条件期望的定义和基本性质 Definition and Basic Properties
在我们举个例子之前我们回忆一下,我们整章都在说的期望,一个随机变量的期望取决于分布,而且我们提到过,不同的随机变量有同样的分布的时候,期望是一样的,那么我们可以进一步说每个分布对应唯一的期望,但是我们知道分布是有条件版本的,所以对应的期望就是条件分布的期望,而期望这个数值在预测过程中满足最小M.S.E. 的要求,所以某些时候用条件期望来预测某个值的出现是合理的。
举个例子:
首先统计了某一个片区所有人家的家庭成员和手机持有数量,然后得到了下面这个表: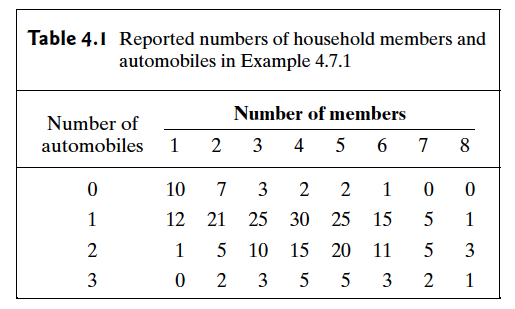
那么当我们随机选取这个调查中的某一家人,其中有n个家庭成员,那么他们的手机持有量是多少呢?
这个问题就是一个典型的预测问题。
Definition Conditional Expectation/Mean.Let $X$ and $Y$ be random variables such that the mean of $Y$ exists and is finite.The conditional expectation(or conditional mean) of $Y$ given $X=x$ is denoted by $E(Y|x)$ and is defined to be the expectation of the conditional distribution of $Y$ given $X=x$ .
这个定义就是条件期望或者条件均值的定义了,如果 $Y$ 存在并且有限,条件 $X=x$ 条件期望 $E(Y|x)$
举个例子
如果Y是一个连续随机变量,给定条件 $X=x$ 其条件p.d.f. $g_2(y|x)$ 那么他的条件期望:
$$
E(Y|x)=\int^{\infty}_{-\infty}yg_2(y|x)dy\text{…………(1)}
$$
同理如果Y是一个离散随机变量,给定条件 $X=x$ 其条件p.d.f. 那么
$$
g_2(y|x)=\sum_{\text{ All }y}yg_2(y|x)\text{………………(2)}
$$
当然上面这个定义对条件有一定要求,因为条件 X也是随机变量,所以其取值也有范围,比如有些情况下 $f_1(x)=0$ 这种情况就很尴尬了,不过也没关系,因为条件发生的概率都是0了,那么在此条件下再发生别的更是不可能,所以这种情况变得无关紧要;另一种尴尬就是$f_1(x)\neq 0$ 也就是条件是某个正常的值了,但是这时候Y可能不存在期望,或者期望是无穷的情况,这时条件期望未定义;
Definition Conditional Means as Random Variables.Let $h(x)$ stand for the function of $x$ that is denoted $E(Y|x)$ in either (1) or (2).Define the symble $E(Y|X)$ to mean $h(X)$ and call it the conditional mean of $Y$ given $X$
想一下,我们前面给出了条件的具体取值,比如当给定 $X=x_0$ 的条件下,$Y$ 的期望是什么。如果我们不给定条件特定的值,那么条件变成一个变量,从微积分的角度来看求条件期望的公式如下
$$
E(Y|X=x)=\int^{\infty}_{-\infty}Yf_1(Y|X=x)dy
$$
如果$X$ 也是变量那么这个两个变量的单积分表达式的结果就是个 $X$ 的函数.
一个🌰 :
临床试验,一定数量的患者接受治疗,只有治愈和未治愈两种结果,假设 $P$ 是大量试验的一个结果统计的成功比例,设 $X_i=0$ 为失败(未治愈) $X_i=1$ 为治愈,并假设 $X_1,X_2,\dots,X_n$ 之间在条件 $P=p$ 之下独立,并有 $Pr(X_i=1|P=p)=p$ ,我们现在来计算X的条件P下的期望,因为 $X$ 是参数为 $p,n$ 的二项分布,所以 $E(X|p)=np$ 以及 $E(X|P)=nP$ 后面我们会计算当我们已知X时如何求 $P$ ,这就是预测问题了
注意,当给定条件 $X$ 时的条件期望 $E(Y|X)$ 是一个随机变量,有自己的分布;给定条件$X=x$ 时,条件概率 $h(x)=E(Y|x)$ 是一函数,这个函数与其他普通函数一样使用;
他们的联系是 $X$ 有一定个概率等于 $x$ 这时候, $E(Y|X=x)=h(x)$ 按照函数 $h$ 来完成计算。
接着我们提出条件版的全概率公式:
Theorem Law of Total Probability for Expectation.Let $X$ and Y be random variables such that Y has finite mean.Then
$$
E[E(Y|X)]=E(Y)
$$
证明:
假设X和Y是连续的随机变量并有一个连续的联合分布
$$
\begin{aligned}
E[E(Y|X)]&=\int^{\infty}_{-\infty}E(Y|x)f_1(x)dx\\
&=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}yg_2(y|x)f_1(x)dydx\\
\end{aligned}
$$
又因为 $g_2(y|x)=f(x,y)/f_1(x)$ 那么就有:
$$
E[E(Y|X)]=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}yf(x,y)dydx=E(Y)
$$
证毕
证明第一步用到了函数的期望,谁是函数?我上面说啦,$h(x)=E(Y|x)$ 可以当做函数使用,然后又用到了条件概率分布和边缘分布的关系,最后得到预料之内的结论。
接下来这个定理反应的是当给定条件 $X=x$ 下的概率,和把 $X$ 当做已知常数 $x$ 是一致的.
Let $X$ and $Y$ be random variables,and let $Z=r(X,Y)$ for some function r.The conditional distribution of $Z$ given $X=x$ is the same as the conditional distribution of $r(x,Y)$ given $X=x$
证明:
当X和Y有一个连续的联合分布:
$$
E(Z|x)=E(r(x,Y)|x)=\int^{\infty}_{-\infty}r(x,y)g_2(y|x)dy
$$
根据前面关于期望的全概率法则,我们有:
$$
E{E[r(X,Y)|X]}=E[r(X,Y)]
$$
证毕
上面这个定理是说当某个随机变量 $Z$ 是另外两个随机变量 $X,Y$ 的某个函数 $r$ 结果,那么当其中一个随机变量 $X$ 或者 $Y$ 被给定为条件的时候 $E(Z|X=x)=E[r(x,Y)|X=x]$
作为期望的第一步扩展,我们这里给出条件方差的定义,当然也有条件距,条件偏度,条件m.g.f,多变量的条件协方差等,篇幅时间都有限,不可能都一一练习,大家要多看例子,不然后面数理统计容易懵逼
Defintion Conditional Variance.For every given value $x$ ,let $Var(Y|x)$ denote the variance ofthe conditional distribution of $Y$ given $X=x$ .That is
$$
Var(Y|x)=E{[Y-E(Y|x)]^2|x}
$$
这就是我们说当给定 $X=x$ 时 $Y$ 的条件期望是 $Var(Y|x)$
条件期望用来预测 Prediction
上面我们临床试验的例子描述了一种场景,并说如果在一个随机样本空间 $n$ (足够大) 中有 $X$ 个成功治愈的样例,那么我们怎么估计 $P$ 这就是一个非常接近数理统计的例子,或者说这就是一个统计了题目。
Theorem The prediction $d(X)$ that minimizes $E{[Y-d(X)]^2}$ is $d(X)=E(Y|X)$
证明过程略复杂,当时我们还是详细的写一下,毕竟后面统计要用到。在证明之前我们先仔细看看这个定理说的到底是个什么事,我们想要预测某个随机变量 $X$ 的某个函数( $d$ )的结果,误差函数被定义为 $[Y-d(X)]^2$ 其结果是 $d(X)=E(Y|X)$
误差函数或者损失函数是机器学习里的名词,这里指的就是类似于前面 M.S.E. 和M.A.E. 的一个指标,最小化时有最优结果。
证明:
我们证明X有一个连续分布,离散分布与连续情况基本一致。
- 令 $d(X)=E(Y|X)$ , $d’(X)$ 是一个任意的预测结果,我们只需要证明 $E{[Y-d(X)]^2}\leq E{[Y-d’(X)]^2}$ 成立
- 根据 $E{E[r(X,Y)|X]}=E[r(X,Y)]$ 有 $Z’=[Y-d’(X)]^2$ 并且 $h’(x)=E(Z’|x)$ 可以把1中的不等式转化成连续函数的期望的形式
$$
\int h(x)f_1(x)dx\leq \int h’(x)f_1(x)dx
$$ - 所以我们就把上面要证明的目标转换成了证明 $h(x)\leq h’(x)$
- 那么我们如果证明了 $E{[Y-d(X)]^2|x}\leq E{[Y-d’(X)]^2|x}$ 就相当于证明了3
- 假定4中的 $x$ 为常数,根据MSE很容易证明结论
证毕
这个证明有点粗糙,但是大概框架给出了,大家需要查阅这两天的博客就能得出完成的证明过程了。
M.S.E. 还和 $Var$ 有关系:当我们预测在给定条件 $X=x$ 的条件下预测 $Y$ 为 $E(Y|x)$ 时其M.S.E就是 $Var(Y|x)$ 如果在 $X$ 未知的情况下最佳预测就是 $E[Y]$
Theorem Law of Total Probability for Variance.If $X$ and $Y$ are arbitrary random variables for which the necessary expectations and variances exist,then $Var(X)=E[Var(Y|X)]+Var[E(Y|X)]$
总结
本文我们介绍了条件版本的期望,然后扩展到了条件版本的方差,以及预测的相关知识。下一篇开始介绍各种各样的分布。
待续
