Abstract: 本文介绍Gamma函数和Gamma分布，本课第二部分介绍指数分布
Keywords: The Gamma Distributions

Gama分布

今天的废话就是如果看书的时候没看透彻，写博客的时候就会不知所言，所以一定要学透了再总结，没学好就总结，会逻辑混乱
本文介绍了另一个非常有用的连续随机变量的分布族——Gamma分布，学习Gamma分布的适用场景和部分性质，以及一个贯穿始终的例子，排队时间，排队不只是人的排队，在计算机高性能计算，比如CUDA中，任务的排队也是有的，所以这个模型适用场景还是比较多的，虽然可能不如正态分布在自然界中那么普遍，但是在正随机变量中，Gamma分布族在连续分布中举足轻重。

伽马函数 The Gamma Function

在提出Gamma分布之前，我们先来认识一个非常有趣的函数，这个函数叫做Gamma函数。
首先来看个例子：
我们在给一灯泡的寿命建模，根据我们经验，这个灯泡的寿命越长，发生的概率越小，时间越短，则概率越高，寿命是0的我们不考虑，我们只考虑从0开始但不包括零，我们用下面的这个模型建模是合理的，之所以说是合理的而不是唯一的，是因为这个模型不具备唯一性：
$$
f(x)=
\begin{cases}
e^{-x}&\text{for} x>0\\
0&\text{otherwise}
\end{cases}
$$
我们在没有大量数据或者试验情况下无法验证模型正确性，但是从目前来看好像和我们知道的先验知识吻合，所以我们就假定其是合理的，然后我们求这个灯泡的均值和方差：
$$
E(X)=\int^{\infty}_{0}xe^{-x}dx\\
Var(X)=\int^{\infty}_{0}x^2e^{-x}dx
$$
注意，第二个方差的计算我觉都有点问题，因为按照这个积分，是把均值当做 $\mu=0$ 来计算的，但是均值是从0到正无穷的积分，所以均值不会是0，所以这个方差公式我们留意一下（如果有人知道我哪错了，可以给我留言，谢谢）
这个均值的计算是一个有趣的函数。
我们来回忆一下，我们的函数都是什么样子的，我们目前学过的函数大多数都是由初等函数经过计算得到的，比如 $e^{x^2+\alpha sin(y)}$ 是指数计算组合了多项式和三角函数得到的一个新函数，当然，我们学了积分，微分运算后，我们可以用积分来生成新的函数，比如，我们把上面求均值的积分，定义为一个新函数，这个函数叫做Gamma函数

Definition 5.7.1 The Gamma Function.For each positive number $\alpha$ ,let the value $\Gamma(\alpha)$ be defined by the following integral:
$$
\Gamma(\alpha)=\int^{\infty}_{0}x^{\alpha-1}e^{-x}dx=1
$$
The function $\Gamma$ defined by Eq.(5.7.1) for $\alpha>0$ is called the gamma function.

这就是Gamma函数的定义，这个希腊字母 $\Gamma$ 读作 “Gamma” 注意，这个函数的自变量是 $\alpha$ 而 $x$ 只是积分中的一个哑变量，没作用，可以写作任何变量。
在举个🌰 ：
$$
\Gamma(1)=\int^{\infty}_{0}x^{1-1}e^{-x}dx=1
$$

上面的例子和接下来内容都说明了 $\Gamma(\alpha)$ 对于所有 $\alpha>0$ 都是有限的。

Theorem 5.7.1 If $\alpha>1$ then
$$
\Gamma(\alpha)=(\alpha-1)\Gamma(\alpha-1)
$$

证明一下这个性质：
因为 $\Gamma$ 是用积分定义的，所以我们现在用分部积分来计算产生上面的定理：
我们令 $u=x^{\alpha-1}$ 以及 $v=-e^{-x}$ 那么我们就会有 $du=(\alpha-1)x^{\alpha-2}dx$ 以及 $dv=e^{-x}dx$ 那么就有
$$
\begin{aligned}
\Gamma(\alpha)&=\int^{\infty}_{0}udv=[uv]^{\infty}_{0}-\int^{\infty}_{0}vdu\\
&=[-x^{\alpha-1}e^{-x}]^{\infty}_{x=0}+(\alpha-1)\int^{\infty}_{0}x^{\alpha-2}e^{-x}dx\\
&=0+(\alpha-1)\Gamma(\alpha-1)
\end{aligned}
$$
使用分部积分法就把原始表达式转化成了一个乘法的递归式。从而证明了结论。进一步根据此性质能推导出下面这条关键性质。

Theorem 5.7.2 For every positive integer $n$ ,
$$
\Gamma(n)=(n-1)!
$$

证明：
对于$n\geq 2$ 我们有：
$$
\begin{aligned}
\Gamma(n)&=(n-1)\Gamma(n-1)=(n-1)(n-2)\Gamma(n-2)\\
&=(n-1)(n-2)\dots1\cdots \Gamma(1)\\
&=(n-1)!
\end{aligned}
$$
因为我们在上面的例子中知道 $\Gamma(1)=1=0!$ 所以结论正确。
证毕

在实际的统计应用中 $\alpha$ 是正整数，或者 $\alpha=n+\frac{1}{2}$ 其中 $n$ 是正整数。
我们来计算下 $\Gamma(n+\frac{1}{2})=(n-\frac{1}{2})(n-\frac{3}{2})\dots\frac{1}{2}\Gamma(\frac{1}{2})$
这个式子的关键是最后那个积分的部分，令 $x=(1/2)y^2$ 那么 $dx=ydy$：
$$
\Gamma(\frac{1}{2})=2^{\frac{1}{2}}\int^{\infty}_{0}e^{(-\frac{1}{2})y^2}dy
$$
代换后里面积分的形状和正态分布一致，但是积分范围不同，正态分布的积分形式是 $\int^{\infty}_{-\infty}e^{(-\frac{1}{2})y^2}dy=(2\pi)^\frac{1}{2}$，所以积分里面的结果是正态分布的一半 $(\frac{\pi}{2})^{\frac{1}{2}}$ 然后有根据正态分布的性质，上面的最终结果是
$$
\Gamma(\frac{1}{2})=\pi^{\frac{1}{2}}
$$

这就是Gamma函数的一些典型用法和数学特性，接下来的定理帮我们提出后面的Gamma分布。

Theorem 5.7.3 For each $\alpha>0$ and each $\beta>0$ ,
$$
\int^{\infty}_{0}x^{\alpha-1}e^{-\beta x}dx=\frac{\Gamma(\alpha)}{\beta^{\alpha}}
$$

为了证明上面的定理成立，我们还是使用变量代换的方法 $-y=-\beta x$ 于是 $x=\frac{y}{\beta}$ 以及 $dx=\frac{dy}{\beta}$ 然后根据定义5.7.1 $\Gamma(\alpha)=\int^{\infty}_{0}x^{\alpha-1}e^{-x}dx$ 得到结论
$$
\begin{aligned}
&\int^{\infty}_{0}x^{\alpha-1}e^{-\beta x}dx\\
&=\frac{1}{\beta}\int^{\infty}_{0}(\frac{y}{\beta})^{\alpha-1}e^{-y}dy\\
&=\frac{1}{\beta^\alpha}\int^{\infty}_{0}y^{\alpha-1}e^{-y}dy\\
&=\frac{\Gamma(\alpha)}{\beta^{\alpha}}
\end{aligned}
$$
本定理是对定义5.7.1的一个扩展，把 $e$ 的指数从 $-x$ 扩展到了 $\beta x$
原书上给出的证明过程有些问题，从第二步到第三步似乎缺少一个负号，或者定理写的就有有问题，缺少一个负号，因为积分中 $x^{\alpha-1}$ 积分结果是 $\infty$ 然后 $e^{\beta}x$ 因为 $\beta>0$ 所以这个积分结果也是 $\infty$ 所以我认为这个公式应该是少了一个负号。(个人认为《Probability and Statistics 4th》影印版 P318 存在错误，所以我给他补上了一个负号，如果我错了，请及时指出)

然后我们继续拿出前面提到的Stirling 公式的另一个版本。

Theorem 5.7.4 Stirling’s formula:
$$
lim_{x\to \infty}\frac{(2\pi)^{1/2}x^{x-1/2}e^{-x}}{\Gamma(x)}=1
$$

这个证明没有给出，我尝试的证明了一下，确实有点困难，所以我们就假装我们会证明就行了。

接下来这个例子非常给力了，会给出Gamma分布的实际用途：
假设一个队列里有 $i=1,2,\dots$ 个顾客，当这个顾客开始被服务时，需要 $X_i$ 个单位的时间，我们假设 $Z$ 是这些顾客的平均速度，我们要建立个模型是在 $Z=z$ 的条件下，$X_1,\dots,X_n$ 的分布(我们的目标)，其中$X_1,\dots,X_n$ 是在 $Z=z$ 条件下的i.i.d（也就是独立同分布）.每个 $X_i$ 的p.d.f. 为 $g_1(x_i|z)=z e^{-zx_i}$ 其中 $x_i>0$ 假设 $Z$ 同样是一个随机变量有分布 $f_2(z)=2e^{-2z}$ 其中 $z>0$ 那么 $X_1,\dots,X_n,Z$ 满足以下关系（i.i.d.的联合分布等于其边缘分布的乘积，条件情况下依旧成立,前面学过的）
$$
\begin{aligned}
f(x_1,\dots,x_n,z)&=[\Pi^{n}_{i=1}g_1(x_i|z)]f_2(z)\\
&=2z^ne^{-z[2+x_1+\dots+x_n]}
\end{aligned}
$$
上式为5.7.11

我们关心的是$X_1,\dots,X_n$ 的分布，$Z$ 在这里只是个条件，所以我们要对 $z$ 进行积分，结合定理5.7.3 $\int^{\infty}_{0}x^{\alpha-1}e^{-\beta x}dx=\frac{\Gamma(\alpha)}{\beta^{\alpha}}$ 让 $\alpha=n+1$ 以及 $\beta=2+x_1+\dots+x_n$ 。再加上定理 5.7.2: $\Gamma(n)=(n-1)!$ 整合 $2z^ne^{-z[2+x_1+\dots+x_n]}$ 。就能得到：
$$
\begin{aligned}
f_n(x_1,\dots,x_n|z)&=\int^{\infty}_{0}f(x_1,\dots,x_n,z)dz\\
&=\frac{2(n!)}{(2+\sum^{n}_{i=1}x_i)^{n+1}}
\end{aligned}
$$

上式为5.7.12
当 $x_i>0$ 时为上面的情况，其他情况为0（我们不要纠结 $g_1(x_i|z)=z e^{-zx_i}$ 和 $f_2(z)=2e^{-2z}$ 是哪里来的）

接下来我们开始Gamma分布，在Gamma分布之前请务必把上面的例子看明白。

伽马分布 The Gamma Distributions

继续上面的例子，我们假设我们得到了n个顾客的服务时间，我们可以很轻松的计算出每个客户的服务速度 $Z$ 我们可以得到 $X_1,\dots,X_n$ 条件下 $Z$ 的条件分布 $g_2(z|x_1,\dots,x_n)$
我们用5.7.11除以5.7.12 并且其中令 $y=2+\sum^{n}_{i=1}x_i$ 我们就能得到：
$$
g_2(z|x_1,\dots,x_n)=
\begin{cases}
\frac{y^{n+1}}{n!}e^{-yz}&\text{for }z>0\\
0&\text{otherwise}
\end{cases}
$$

这个例子中的p.d.f.就是我们今天要研究的对象，Gamma分布。

Definition 5.7.2 Gamma Distributions.Let $\alpha$ and $\beta$ be positive numbers.A random variable $X$ has the gamma distribution with parameters $\alpha$ and $\beta$ if $X$ has a continuous distribution for which the p.d.f. is
$$
f(x|\alpha,\beta)=
\begin{cases}
\frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x}&\text{ for } x>0\\
0&\text{otherwise}
\end{cases}
$$

根据定理5.7.3 结果是1.
Gamma分布长这个样子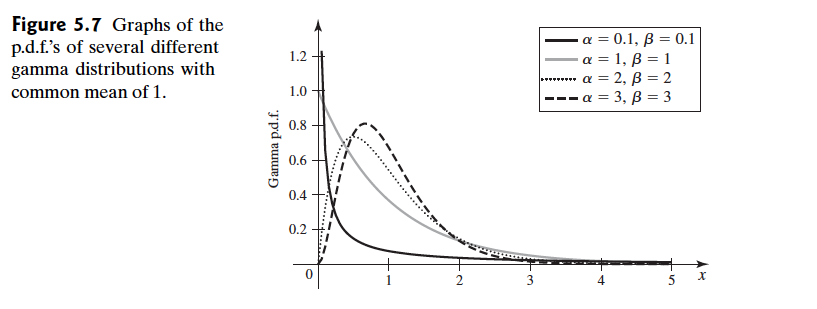

接着我们研究一下gamma分布的距，进而能得到均值和方差。

Theorem 5.7.5 Moments.Let $X$ have the gamma distribution with parameters $\alpha$ and $\beta$ For $k=1,2,\dots$
$$
E(X^k)=\frac{\Gamma(\alpha+k)}{\beta^k\Gamma(\alpha)}=\frac{\alpha(\alpha+1)\dots(\alpha+k-1)}{\beta^k}
$$
In particular $E(X)=\frac{\alpha}{\beta}$ , and $Var(X)=\frac{\alpha}{\beta^2}$

证明：
$k=1,2,\dots$ 然后我们有
$$
\begin{aligned}
E(X^k)&=\int^{\infty}_{0}x^kf(x|\alpha,\beta)dx\\
&=\frac{\beta^\alpha}{\Gamma(\alpha)}\int^{\infty}_{0}x^{\alpha+k-1}e^{-\beta x}dx\\
&=\frac{\beta^\alpha}{\Gamma(\alpha)}\cdot \frac{\Gamma(\alpha+k)}{\beta^{\alpha+k}}\\
&=\frac{\Gamma(\alpha+k)}{\beta^k\Gamma(\alpha)}
\end{aligned}
$$
然后就能得到结论了，包括均值和方差。

Theorem 5.7.6 Moment Generating Function.Let $X$ have the gamma distribution with parameters $\alpha$ and $\beta$ .The m.g.f. of $X$ is
$$
\psi(t)=(\frac{\beta}{\beta-t})^\alpha \text{ for }t<\beta
$$

证明如下：
$$
\psi(t)=\int^{\infty}_{0}e^{tx}f(x|\alpha,\beta)dx=\frac{\beta^\alpha}{\Gamma(\alpha)}\int^{\infty}_{0}x^{\alpha-1}e^{-(\beta-t)x}dx
$$
上述积分在 $t<\beta$ 时是有限的，那么当 $t<\beta$ 时：
$$
\psi(t)=\frac{\beta^\alpha}{\Gamma(\alpha)}\cdot\frac{\Gamma(\alpha)}{(\beta-t)^{\alpha}}=(\frac{\beta}{\beta-t})^\alpha
$$

然后就能得到结论，有同样参数 $\beta$ 的gamma分布的独立的随机变量，他们的和还是gamma分布。

Theorem 5.7.7 If the random varibale $X_1,\dots,X_n$ are independent,and if $X_i$ has the gamma distribution with parameters $\alpha_i$ and $\beta(i=1,\dots,k)$ ,then the sum $X_1+\dots+X_k$ has the gamma distribution with parameters $\alpha_1+\dots+\alpha_k$ and $\beta$

根据m.g.f.的性质，独立的随机变量的和的m.g.f.是其m.g.f.的积，那么我们证明如下：
$$
\psi_i(t)=(\frac{\beta}{\beta-t})^{\alpha_i} \text{ for }t<\beta\\
\psi(t)=\Pi^{k}_{i=1}\psi_i(t)=(\frac{\beta}{\beta-t})^{\alpha_1+\dots+\alpha_k} \text{ for }t<\beta
$$
那么我们就可以看出这个 $\psi$ 对应的也是gamma分布，其中 $\alpha=\alpha_1+\dots+\alpha_k$ 并且 $\beta$ 不变。

总结

至此我们大概的学习了一下 Gamma分布，下一篇我们继续从Gamma上扩展出指数分布。
待续。。