Abstract: 作为第一章的开篇文章，本文从数理统计学的由来开始，大致的说了一下整体的数理统计学的发展，后面逐一展开，进行介绍。
Keywords: 《推测术》，早期概率论，赌博

早期概率论——从萌芽到《推测术》

本文开始介绍数理统计学简史，信息基本全部来自陈希孺老师——《数理统计学简史》，这本书目前已经没有在售了，所以尽量将原始信息归纳总结，然后以博客的形式发到网上，后来之人可以阅读，也算是对知识的传承了。
本篇作为第一章的开篇，讲的非常大，都是框架性的东西，所以，追求细节是后面的事情，现在我们要做的是根据这些概念间的关系，逐步构建起整个知识结构，通过他们的发展过程，这无疑能帮助我们加深对知识的理解，本系列每篇都会配图，最后会用一个时间轴来总结全部知识点，希望大家多多访问，多多留言！
本系列计划每日一篇，敬请期待。。

概率到事件

概率是什么

概率是一件事发生，一种情况出现的可能性大小的数量描述，你可以用文字的可能，非常可能，肯定可能来描述一件事情的发生可能性，但是没办法进行更细致的比较，因为你用的这些描述语，说到底也是离散的，所以，我们想用一种连续的方法来描述，数量是一个很好的方法，把不同的可能性程度对应到不同的数字上去，而这些数字，我们规定从0到1，当然，也可以从0到100，但是前辈们没那么选择，所以我们还是从0到1吧
上面这种数字描述概念最早出现在 16世纪 与掷骰子密切相关，最早的概念已无法追溯。

“可重复性” vs “一次性”

事件分“可重复性” 和 “一次性”之分。第一种是可以重复进行的，比如扔骰子，原则上在一定条件下，可以多次的重复该事件，但是永远不能做到无限次。一次性的，明显，这个事就一次，比如明天是2018年4月22日上午8点下雨，这事到明天8点整就可以确定发没发生了，而且不可重复，就一个2018年4月22日上午8点（除非时间逆转）
当然，第一种说的重复进行的事件是控制在一定条件下的，这个我其实是有疑问的，因为根本没办法控制，最简单的，我认为温度和湿度会影响扔骰子，首先你没有证据证明我这个怀疑是无效的，所以，因为温度湿度根本不可控制，所以没办法控制条件完全一致，只能说相对一致。
我们把可重复性的事件概率叫做客观的，一次性的事件成为主观的。客观概率有一定的依据，不会随人的意志转义，主观完全随人的意志转移。
哲学家有不同的观点，主观概率随人的意志转移的根本原因是人的知识不够全面，如果人对这件事的知识完全掌握，主观概率只有0，1两种情况，比如目前来看，我问你火星有生命么？你可能说有万分之一的可能性有，明显，这个回答目前来说是没什么问题的。但是如果有一天我们完全掌握了火星，那么这个概率就会变成0或者1，有就是有没有就是没有，只是我们现在没有弄清楚而已。
逻辑学家和神学家也在研究主观概率。

客观概率

可重复的事件产生客观概率，而客观概率有开始分成了两种形式：

统计概率

因为事件可重复，所以经过大量试验后，事件出现的频率，可以被估计成该事件的概率，这一点非常直观，但是估计就会有所不同，比如某地12岁以下的儿童有100万，其中5000人得了某种疾病，我们就可以说该地区12岁以下儿童发病概率是0.005，这是一种估计，但显然这个估计准不准，值得商榷，所以用这种方法来定义概率也有点说不通，因为定义要保证一致性，不能一个事物的定义会经常发生变化，这是不对的。但是种方法的客观性还是值得肯定的，毕竟不是某个大神自己评估出来的，比如我国有 $95\%$ 的好人，这就是不客观的！
上面的定义形式好处是得到的结果比较能得到人们的认同，没有主观意见在里面，但是作为定义似乎又不太合适。
这种概率的定义方式被叫做统计概率

古典概率

试验结果数量有限，而且每种结果出现机会均等，不存在谁比谁高或者低的暗示，那么如果结果有 $N$ 个，那么这种结果出现 $M$ 次的概率就是 $\frac{M}{N}$ 比如均匀的骰子，这个均匀就暗示每种结果出现等可能，所以，扔出3的倍数的情况只有两种 3，6，那么相当于结果出现了2次，一共6种结果，概率为 $\frac{2}{6}$ 如果骰子不均匀，以上所有结论轰然倒塌。
这种概率的定义方式被叫做古典概率

Kolmogorov拯救概率

1933年 苏联大数学家柯尔莫哥洛夫提出了公理化的定义方式，这种定义方式不会和上面任何派系产生冲突，而是只定义了概率的几条规则，而根本不说什么是概率.
而客观主观概率的计算都遵守上面的公理，而本质是啥，他们会继续争下去。

“贝叶斯学派” vs “频率学派”

主观概率和客观概率在数理统计中有非常重要的地位，不要以为主观概率完全是瞎说，主观概率产生了贝叶斯学派，后面会详细介绍，这个学派的很多思想我是非常赞同的，而另一派是频率学派，也就是客观概率的学派，客观学派目前占领了数理统计的大部分阵地。

赌博到骰子

古典概率试用的典型场合是扔骰子，骰子出现在 公元960年左右，怀特尔德大主教，计算了三个骰子的不计顺序的组合数，56种情况，三颗相同的6种，两颗相同另一颗不同的30种，都不同的20种，

14世纪 骰子赌博成风，纸牌到1350年才出现记载，由于教会反对，和国家禁止，直到18世纪初纸牌才取代骰子，称为主要的赌具。
纸牌的情况更复杂，促进了概率论的发展。

卡丹诺

公元960年左右文艺复兴前概率还不算数学概念。

16世纪初意大利数学家讨论掷骰子中各种情况出现的可能性。这些研究结晶出了古典概率定义：把要研究的情况分解成一些看似同等可能的简单情况，其数目与全部可能结果数之比，即取为该情况出现的概率。这个说法最初出自谁人已经无法考证，但是，现在为人所知的一位叫做，卡丹诺(G.Cardano 1501~1576)，把古典概率的发明归功于他的名下也许无人反对。

总结

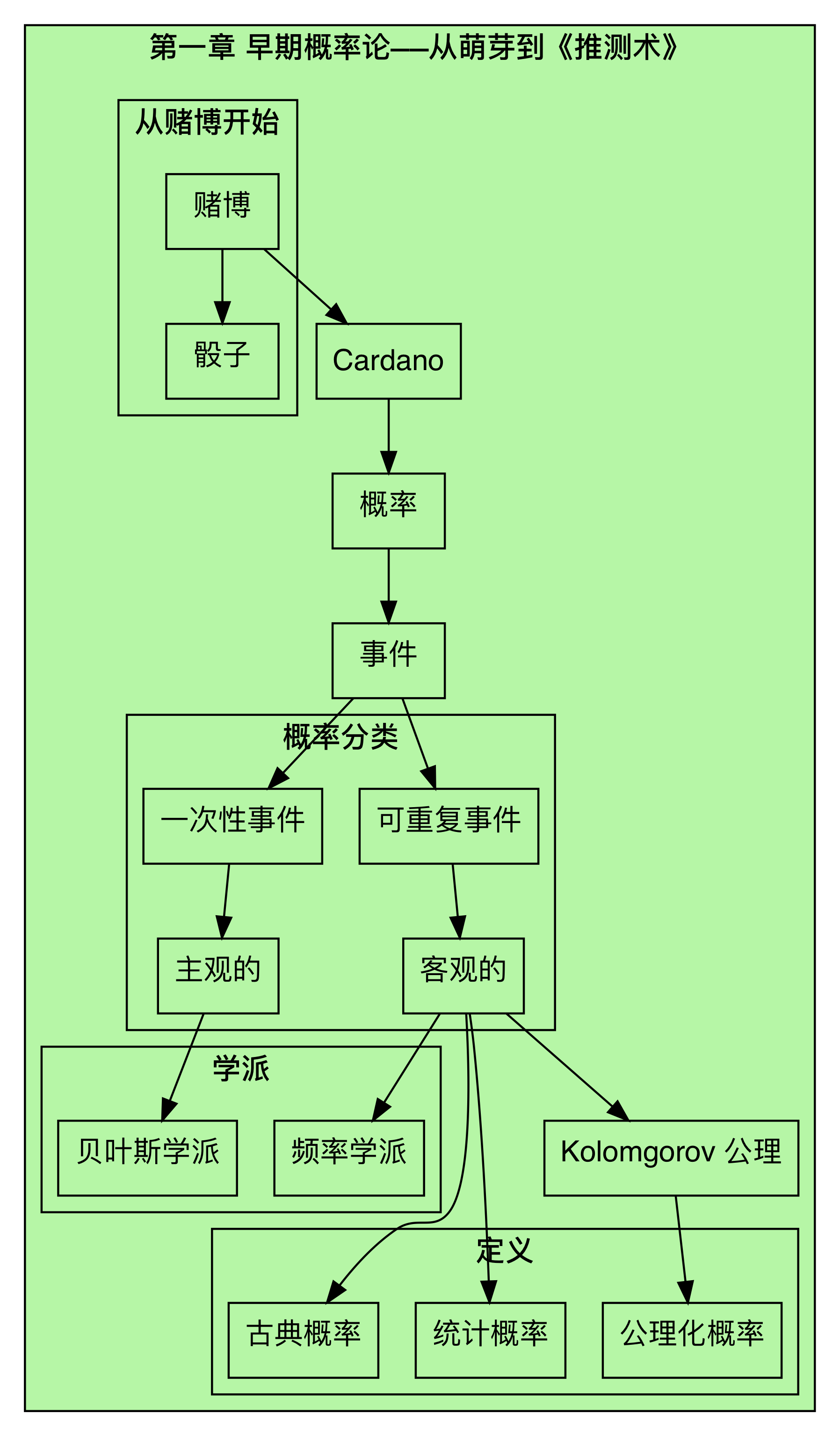
上面这个图是我大概本篇的大概归纳，如有不妥，还望各位指点。